《图论导论》定义与案例
图的定义与基础概念
图的组成:节点集[V(G)],边集[E(G)]
flowchart LR
Graph --> vertices(["V(G)"])
Graph --> edges(["E(G)"])
vertices --> ver_example["格式示范:u"]
edges --> ed_examples["格式示范:u,v; 外加大括号"]
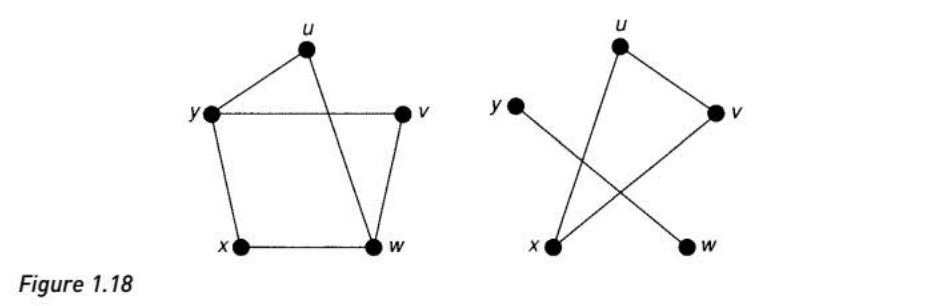
图的重构(Isomophism)
图的重构可以采用如下的数学逻辑描述:
\[for \ G_1 \ and \ G_2, E_1(G) \leftrightarrow E_2(G)\]图的连接(Connected Graph)
图的连接可以采用如下的数学逻辑描述:
\[\begin{aligned} & G_{connected} = G_1 \bigcup G_2 \\ & \to E(G_{connected})=E(G_1)\bigcup E(G_2) \\ & \to V(G_{connected})=V(G_1)\bigcup V(G_2) \end{aligned}\]相邻(Adjacency)与度(Degree)
- 节点相邻(adjacent vertices):存在共边
- 边相邻(adjacent edges):存在共节点
- 孤立点(isolated vertex):度为0的点
- 终止点(end vertex):度为1的点
度序列:以升序/降序形式表示每个节点度分布的方式,写作(min degree, …, max degree)
握手引理(Handshake Lemma)
任何图中,所有节点度之和为偶
证明:节点度之和等于边的两倍,因此必为偶
握手引理(Handshake Lemma)的推论
任何图中,奇数个分支的节点数为偶
证明:如果奇数个分支的节点数为奇,则图中所有节点度之和为奇,与握手定理矛盾,因此不存在
子图(Subgraph)
子图可以采用如下的数学逻辑表述:
\[H \in G, if \ V(H) \in V(G) \ and \ E(H) \in E(G)\]注意点:两种子图
第一类子图:$G-e$,代表去掉$e$这条边
第二类子图:$G\ e$,代表将$e$两侧的节点融合成一个节点
简单图的补(Complement Graph)
简单图的补用数学公式表示为$\overline{G}$,$\overline{G}$边的分布情况和图$G$是刚好相反的
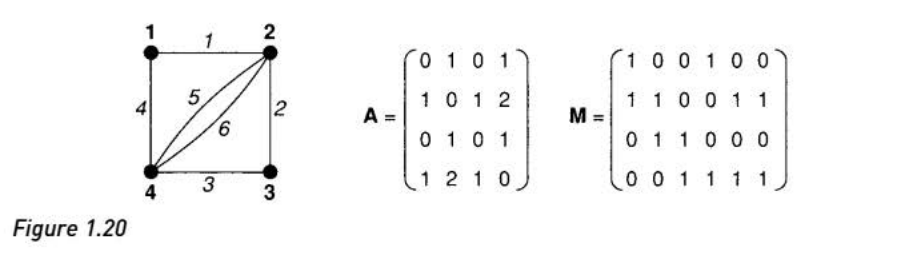
图的矩阵表示
分为两种:
- 邻接矩阵(adjacency matrix):$n \times n$
- 关联矩阵(incidence martrix):$n \times m$
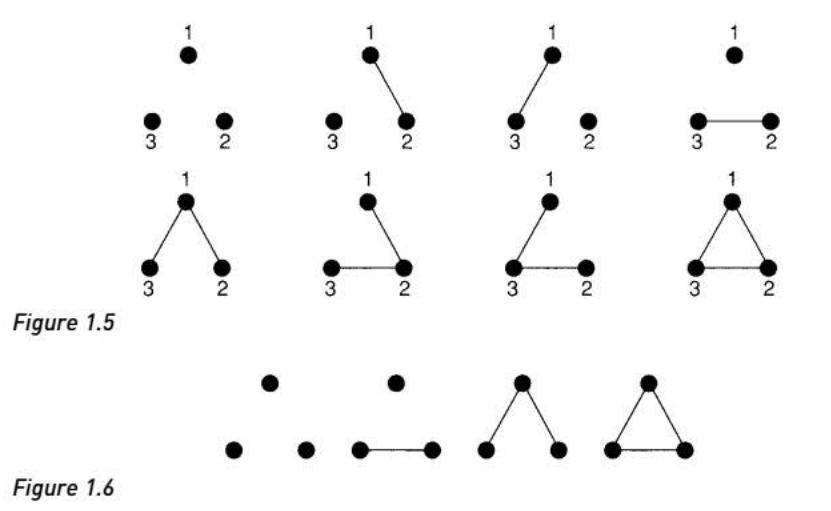
一些特殊的图
- 无边图(null graph):边集为空集的图,对于有n个顶点的无边图可以用$N_{n}$表示
- 完全图(Complete graph):所有顶点都两两相连的图,对于有n个顶点的完全图可以用$K_{n}$表示
- 环图(Cycle graph),路径图(Path graph),轮轴图(Wheels):对于有n个顶点的图分别表示为$C_{n},P_{n},W_{n}$
- 规则图(Regular graph):每一个顶点都具有度$r$的图
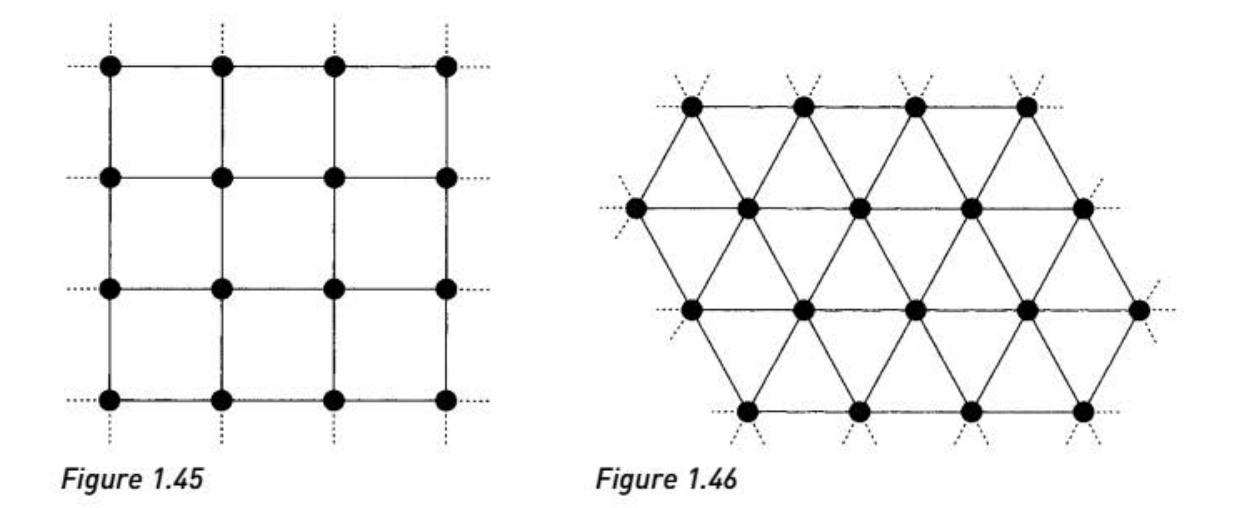
- 柏拉式图(Platonic graph):对应于柏拉图立体(Platonic solids)的骨架图(skeleton graph),每个顶点代表一个立体的顶点,每条边代表一个立体的边
- 二分图(bipartite graph):可以被解耦为两部分顶点,且两部分顶点间的连接和原始图一致的图,记作$G=G(A,B)$
完全二分图是指,两部分顶点间均只有一条边相连的图
- k方图(k-cubes):顶点表示所有长度为 k 的 二进制串(0/1)的图,表示为$Q_{k}$,该图两顶点之间有一条边当且仅当它们的二进制表示恰好相差一位
有向图(Digraph)
有向图及其节点与边分别可以表示为:$D$, $V(D)$, $A(D)$(有向边,arcs);有向图的出度被称作out-degree,入度被称为in-degree
有向图入出度平衡定理(handshaking dilemma, Directed Graph Degree Sum Formula)
在任何有向图中,出度均等于入度
证明:出度等于有向边数,入度等于有向边数,因此出度等于入度
反转图(converse graph):把原图每条有向边(arc)的方向全部反转得到的新图,表示为$D’$
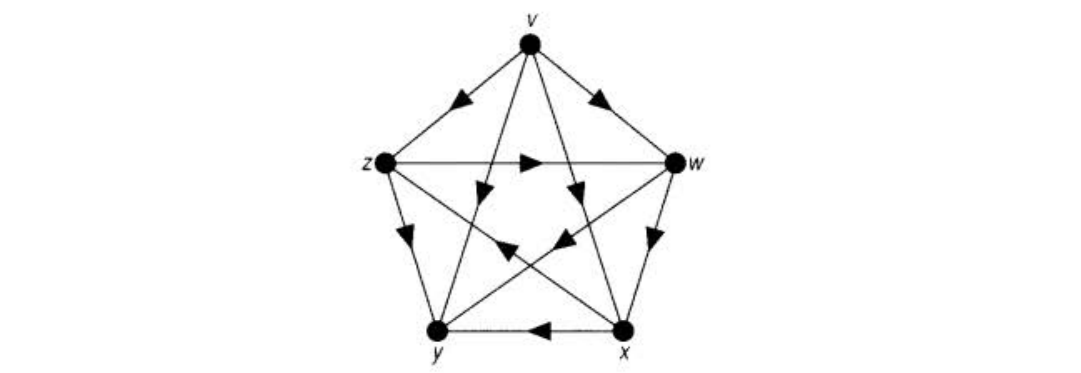
竞赛图(Tournament)
一种特殊的有向图,该种有向图的每个节点对间都有一条有向边连接
无穷图(Infinite Graph)
无穷图包含无穷点集$V(G)$和无穷边集$E(G)$,若二者都可数无穷(countable infinite),则无穷图被称作可数图(countable graph)
不考虑的两种情况
情况一:节点有穷,边无穷,图中出现回环
情况二:节点无穷,边有穷,图中出现孤点
- 无穷图的局部有穷(locally finite)特性:当一个无穷图中的每个节点都含有有穷边的情况下,则称该无穷图局部有穷
- 无穷图的局部可数(locally countable)特性:当一个无穷图中的每个节点都含有可数边的情况下,则称该无穷图局部可数
有穷和可数的关系
局部有限(locally finite):要求无穷图中每个顶点的度数是有限的
局部可数(locally countable):允许每个顶点的度数是可数无限的(包括有限或ℵ₀)
局部有限图必然是局部可数的,但局部可数图不一定是局部有限的,即$locally \ finite ⊂ locally \ countable$
无穷图的两个理论
- 每个局部连接可数的无穷图是可数图
证明:任选无穷图中的一个节点$v$,令$A_1$为$v$周边节点的集合,$A_2$为$A_1$周边节点的集合,以此类推,由于这里每一个集合都是可数的,因此这些集合的并集也可数,因此整个无穷图可数 - 每个局部连接有限的无穷图是可数图
证明方法类似,不再赘述
图论三谜题(Three Puzzles About Graph)
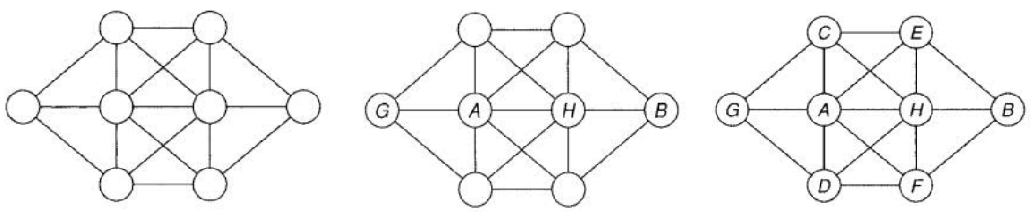
字母填坑问题(The Eight-Circles Problem)
题目:A,B,C,D,E,F,G,H八个字母放到下图八个圆中,保证每两个相邻圆节点无相邻字母
方法:A,H最特殊,可以放在最麻烦的地方;放完后紧邻着快速放B,G,然后快速填完其它字母
六人聚会(Six People at a Party)
证明:任何六人聚会中,要么三个人互不相识,要么三个人都互相熟知
方法:
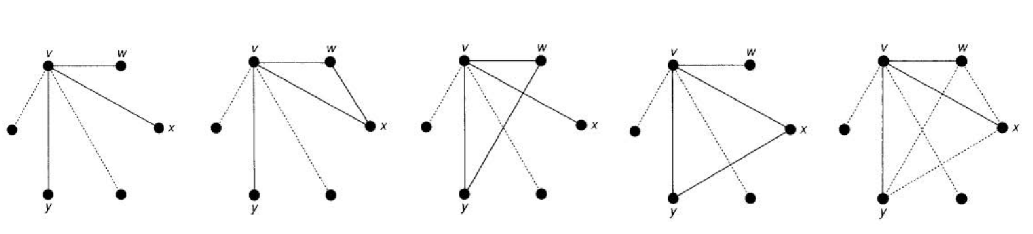
- 节点间的连接关系仅有两种,要么是认识,要么是不认识;因此用两种线表示,实线表示认识,虚线表示不认识;则要证明的命题转化为求证图中必然存在一个实线三角形或一个虚线三角形。
- 然后从6个顶点中随便选一个,找到切入点,和其余5个顶点有5条连线;又由鸽巢原理,至少三条线同类型,即至少三条线是是实线或者虚线
- 不妨假设三条线都是实线,观察这三条实线连接到的三个点,这三个点之间的连接状态分为三种
- 第一种为存在一条实线,直接得到存在实线三角形,证明完毕
- 第二种为没有一条实线,则这三点得到虚线三角形,同样证毕
- 三条线都是虚线时同理,因此完成证明
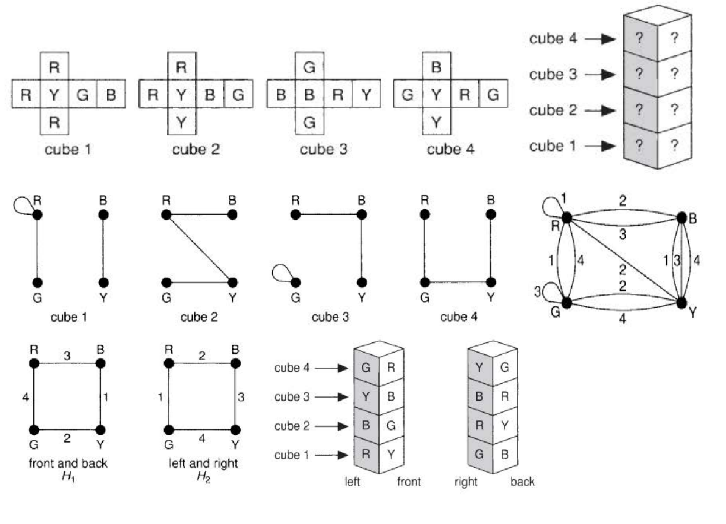
四方问题(Four-cubes Problem)
题目:四个方块的颜色被涂上红、蓝、绿、黄,如何堆才能堆出四种颜色都出现在一面的 $4\times 1$ 长方体
方法:
- 将四种颜色视为四个不同节点,立方体中的相对面视作边,从而构建一个网络
- 将第一步中四个立方体对应的四个图合并称一个图,并在每个边上标记所属立方体
- 然后在第二步的图中找到四节点环形结构,既可以得到对应四方问的题解方案