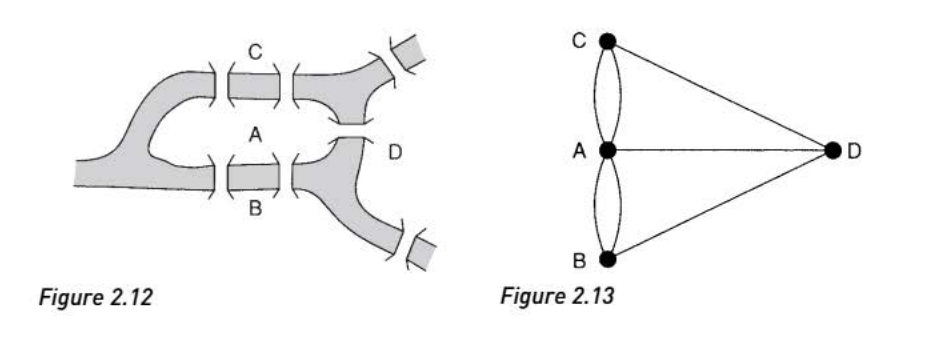
《图论导论》路径和环

连通性前置知识

• 游走(walk)：从$v_0$到$v_m$的过程，写作 $v_0 \to … \to v_m$
• 起始节点(initial vertex)
• 末端节点(final vertex)
• 游走长度(walk)：从$v_0$到$v_m$的边数

不同种类的游走

• 轨迹(trail)：无重合边的游走
• 路径(path)：无重合边和重合点的游走
• 闭轨(closed trail)：首尾相接的轨迹
• 环(cycle)：首尾相接的路径

连通图的性质

• 性质一：当且仅当如果图G的每个环都为偶数长度，G为二分图

  证明
  充分条件：对于环 $v_0 \to … \to v_m$，从$v_0$到$v_1$到$v_2$才能实现回环，因此为偶数长度
  必要条件：如果要在二分图中成环，至少需要从A到B再到A，因此为2的倍数，故为偶数长度

• 性质二：对于有n个节点的简单图，边m的取值范围为 $n-1 \le m \le \frac{1}{2}n(n-1)$
• 性质三：对于有k部分n个节点的简单图，边m的取值范围为$n-k \le m \le \frac{1}{2}(n-k)(n-k+1)$

  证明
  最少边的时候不存在环，仅有k部分非闭合路径，各部分合起来即 $n-k$ 条边
  最多边的时候每部分都有环，这里可以通过等效，先挪出 $k-1$ 个孤立节点形成 $k-1$ 个部分，则最后一大部分剩 $n-k+1$ 个节点，每个节点和 $n-k$ 个节点相连，形成 $\frac{1}{2}(n-k)(n-k+1)$ 条边
  故m的取值范围为$n-k \le m \le \frac{1}{2}(n-k)(n-k+1)$

连通性重要定理

连通图连通性的相关定义

• 解连集(disconnecting set)：一组删除后能让图不再连通的边集
• 分离集(separating set)：一组删除后能让图不再连通的点集
• 割集(cutset)：最小解连集
• 桥(bridge)：只有一个元素的割集
• 割点(cut vertex)：分离集中的元素

非连通图连通性的相关定义：

• 边连通指数$\lambda(G)$(edge-connectivity)：图G最小割集的元素数
• k边联通(k-edge-connected)：至少需要移除k条边才能断开的图，数学表示为$\lambda(G) \ge k$
• 点连通指数$\kappa(G)$(connectivity)：图G最小分离集数

• k点连通(k-connected)：至少需要移除k个点才能断开的图，数学表示为$\kappa(G) \ge k$

• 性质四(Menger, 1927)：当且仅当图G中的任意两个节点间由不存在共边的至少k条路径相连，则称图G是k边联通的

  证明
  充分条件：如果存在k条路径相连，只可能在去掉k条边时G被解连，因此图G是k边连通的
  必要条件：如果图G是k边连通的，那么一定存在一个节点对间有k条路径相连，且其他节点对的边数大于等于k

• 性质五：当且仅当任意两个节点间存在至少 $k+1$ 条内部顶点不重叠的路径，则称图G是 $k+1$ 点联通的

  证明
  充分条件：如果存在 $k+1$ 条路径内部顶点不重叠，只可能在去掉 $k+1$ 条路径时G被解连，因此图G是 $k+1$ 点联通的
  必要条件：如果图G是 $k+1$ 点联通的，那么一定存在一个节点对间有 $k+1$ 条路径内部顶点不重叠，且其他节点对的相应路径数大于等于k

• 性质六：对于任意图，都有$\kappa(G) \le \lambda(G) \le \delta(G)$，其中$\delta(G)$为最小的节点度

  证明
  $\kappa(G) \le \lambda(G)$：假设改图本身没有被隔断，则对于每个节点都有至少一条边，故只需要删除少量节点使图不连通，而对应要删除更多的边为代价，因此$\kappa(G) \le \lambda(G)$
  $\lambda(G) \le \delta(G)$：使得图本身被隔断，只要删除一个节点的所有度，自然可以实现；因此删除所需的最大边数即最小的节点度

有向图连通性的相关定义：

• 强连通(strongly connected)：图G中任意两个节点v和w间都存在有向路径相连

  案例：如从节点A能到节点B，从节点B也能到节点A

可定向与定向

• 可定向(orientable)：如果一个图在赋予方向后，其可变为强连通图，则成为该图可定向
• 定向(orientation)：如果改图可定向，则称得到的有向图为该图的定向

罗宾引理(Robbin Lemma)
一个非定向连通图能够被定向为强连通有向图，当且仅当它是2-边连通(无桥)

• 性质六：当且仅当每个边都在某个环中，该图是强连通的

  证明
  充分条件：如果存在一条不在环中的边，则该边作为桥(bridge)而存在，自然该图不会可连通
  必要条件：如果图可连通，则对于任意两个节点都存在双向通路，在该条双向通路上的每条边自然都是在环里的

无穷图的连通性

概念延申：

• 有穷游走(infinite walk)：如前文所述，无更新
• 单向无穷游走(one-way infinite walk)：写作$v_0 \to v_1 \to …$

• 双向无穷游走(two-way infinite walk)：写作$v_{-2} \to v_{-1} \to v_0 \to v_1 \to …$

• 性质七(König, 1927)：令图G为连通且局部有穷的无穷图，则对任意G中节点v，都存在一条以v为初始节点的单向无穷游走

  证明：其实不难，从中取一节点，由于局部有穷，其必然可连接至一周边节点，以此类推即可形成一个单向无穷游走

欧式图和欧式有向图

欧式无向图(Eulerian Graphs)

欧式图的起点
欧式图起始于过桥问题，即如何不重复的经过所有桥仅一次并在最后回到起始点；而后也逐渐延申为了一笔画问题，即不重复遍历图中所有的边

欧式图(Eulerian)定义及拓展：若图G存在一条能包含所有边的闭合迹，则称该图为欧式图(Eulerian)，该闭合迹则被称为欧式迹(Eulerian trail)，如果存在一条能包含所有边的非闭合迹，则称该图为半欧式图(semi-Eulerian)

欧式图引理：如果图G每个节点的度不小于2，则图G存在一个环

证明
首先对图进行简化，当存在自环(loop)或者多边时，矛盾；因此只考虑简单图
对于简单图，可以构建游走(walk) $v_1 \to … \to v_k$，由于每个顶点的度都不小于 2，我们总可以从当前路径的末端延伸出一条新边，前往一个新的顶点；图是有限的，因此路径不能无限延申下去。最终我们将回到某个已经访问过的顶点，从而形成一个环；所以，在每个顶点的度数都不小于 2 的有限简单图中，必存在一个环
注意：该引理仅适用于有穷图；当为无穷图时，可以无穷延申而不回头

欧式图判定定理：当且仅当图连通且图中每个节点的度都为偶数时，该图为欧式图

证明
充分条件：每个节点的度都为偶数，由欧式图引理，任选一个节点可绘制闭合路径，记为$C_1$；若该路径覆盖整个图，又考虑到该图中每个节点的度都为偶数，则该图为欧式图；当路径不覆盖整个图，则从$C_1$中任意节点为起点，又可以绘制新闭合路径，记为$C_{new}$；这些路径综合在一起仍然可以形成欧式图，证毕
必要条件：图为欧式图，因此存在一条回路$C$，该回路中的节点有进必有出，因此其的度为偶数；同时该图必须连通，不然无法满足欧式图的条件；故欧式图连通管且每个节点的度都为偶数

欧式图推论

• 推论一：当且仅当连通图的边集可被拆分为具有非共享边的环(cycle)时，该连通图为欧拉图

  证明
  拆分为具有非共享边的环，等效为从$C_1$中的任意节点为起点绘制出$C_{new}$，证毕

• 推论二：当且仅当连通图恰好有两个节点的度为奇数时，该连通图为半欧拉图

  证明
  恰好有两个节点度为奇数，该图的迹则需从一个奇数度节点起到另一个奇数度节点止，即绘制出了半欧拉图

欧式图的迹构建理论

从任意节点u开始对边以任何一种方式进行遍历，遵循如下规则：

• 法则一：擦除经过的任何一条边，以及因此而产生的任何孤立点
• 法则二：在每一步中，只有在没有其他选择的时候，才走桥边(bridge)

证明
在一张连通且所有点度数为偶数的图中，若每一步仅在无其他选择时才经过桥边，则从任一点出发始终可以依次遍历所有边恰好一次并回到起点，因每次走非桥边可保持图连通性，桥边仅在必要时才断开图，使路径最终闭合，构成欧拉回路。

欧式有向图(Eulerian Digraphs)

欧式有向图(Eulerian digraphs)的定义：当连通有向图$D$存在包含$D$中每条有向边(arc)的闭合有向迹，则称该有向图为欧式有向图；该闭合有向迹则被称为欧式迹(Eulerian trail)

欧式有向图判定定理：当且仅当连通有向图$D$每个节点的出度等于入度时，该图为欧式有向图

证明
充分条件：入度等于出度时，必然可以找到一个环，该环若完全覆盖整个有向图，则直接成立；若不完全覆盖，在路径中的任意节点基础上可以继续得到一个新环，将所有这些环叠加即可形成一个欧式有向图
必要条件：该图为欧式有向图，对于每个节点入度后必然会出度，因此每个节点的入度和出度相等

欧式无穷图(Infinite Eulerian Graphs)

对于一个可数连通的欧式无穷图(countable connected graph which is Eulerian)，其必须满足：

• G中没有节点具有奇数度
• 对于图G中的任意一个有限子图H，我们从G中删去H的所有边，得到新的图K。那么这个新图K至多会被分成两个无限连通部分(infinite components)
• 如果再额外要求：H中每个顶点的度数都是偶数，那么删除H的边后，图K只剩下一个无限连通部分

证明
性质一：若存在奇数度顶点，则在遍历所有边的欧拉路径中，该点的进出次数不平衡，导致路径无法封闭或继续，故矛盾。
性质二：若删除有限边集后剩余图中出现三个以上无限连通分量，则任一欧拉迹需从有限子图中分别进入至少三次，违反路径连续性与边数有限性，故矛盾。
性质三：若删去偶度子图后图变为多个无限分量，则欧拉迹需从偶度顶点多次进出连接多个部分，破坏其偶度结构，违背欧拉路径存在性，故矛盾。

汉密尔顿图和汉密尔顿有向图(Hanmiltonian Graph and Digraph)

汉密尔顿图(Hanmiltonian Graph)

定义：设图G是一个无向图，若存在一条通过图中每个顶点恰好一次，并且首尾相接的回路(cycle)，则该回路称为汉密尔顿回路（Hamiltonian cycle），图G被称为汉密尔顿图（Hamiltonian graph）；若图G不含汉密尔顿回路，但存在一条通过所有顶点恰好一次的路径(path)，则称G为半汉密尔顿图（semi-Hamiltonian graph）。

汉密尔顿图的判定(Ore, 1960)：设G是节点数大于3的简单图，若对图中每对不相邻节点v和w都存在$deg(v)+deg(w) \ge n$，则图G是汉密尔顿图

证明
存疑，后续补充

汉密尔顿图判定的推论(Dirac, 1952)：设G是节点数大于3的简单图，若对图中每个节点v都存在$deg(v) \ge \frac{1}{2}n$，则图G是汉密尔顿图

汉密尔顿有向图(Hanmiltonian Digraph)

定义：设图G是一个有向图，若存在一条通过图中每个顶点恰好一次，并且首尾相接的有向回路(cycle)，则该回路称为汉密尔顿有向回路（Hamiltonian cycle），图G被称为汉密尔顿有向图（Hamiltonian graph）；若图G不含汉密尔顿回路，但存在一条通过所有顶点恰好一次的有向路径(path)，则称G为半汉密尔顿有向图（semi-Hamiltonian graph）

汉密尔顿有向图的判定：设具有n个节点的有向图D强连通，如果每个节点$outdeg(v) \ge \frac{1}{2}n \ \& \ indeg(v) \ge \frac{1}{2}n$，则该有向图为汉密尔顿有向图

汉密尔顿有向图的特殊应用

• 每个非汉密尔顿竞赛图都是半汉密尔顿有向图
• 每个强连通竞赛图都是汉密尔顿图

路径与环的应用(Applications)

• 最短路径问题(Shortest Path)

  • 目标：在加权图（每条边有非负权重）的两个顶点之间，找到总权重最小的路径。
  • 经典算法：Dijkstra 算法，通过“从起点逐步松弛标签”得到最优距离标签。
  • 特点：时间、成本、距离等多种现实意义都可转化为“权值”。

• 关键路径问题(Critical Path)

  • 背景：项目管理中的活动调度，使用有向加权图表示任务流程与耗时。
  • 目标：找出从“开始”到“结束”的最长路径，即项目的完成时间。
  • 方法：类似 Dijkstra，但取最大标签；正向计算最早完成时间，反向求最晚期限。

• 中国邮递员问题(Chinese Postman)

  • 任务：在加权无向图中找到一条闭合路径，覆盖每条边至少一次，总权重最小。
  • 解决策略：如果图为 Euler 图，可直接找到欧拉回路；否则先找最短路径配对奇点，或称“最小成本配对”。
  • 特别情况：如仅有两个奇点，则可先找半欧拉路径，再加入最短补路，构造最优闭合路径。

• 旅行商问题(Travelling Salesman Problem)

  • 情境：完全加权图中，需找 Hamilton 回路覆盖所有顶点，总权重最小。
  • 复杂性：NP 难问题；暴力枚举（所有回路）复杂度 ~ (n–1)!/2，快速失效。
  • 实用方案：目前没有多项式-time 精确解；常采用启发式算法寻近似最短解。