《图论导论》平面图
平面图(Planar Graph)的基本知识
平面图(planar graph)的定义：平面图是指不存在交叉(crossing)、能被完整体现在平面(draw in the plain)上的图。
瓦格勒(Wagner,1936)-珐里定理(Fáry,1948)：一个简单平面图的任意边都是直线。
交叉数
在平面上绘制一个图 G 时，所需要的最少的边的交叉数量；如对于平面图，交叉数为0
库拉托斯基(Kuratowski)定理：一个图是平面图，当且仅当它不包含任何与 $K_5$ 或 $K_{3,3}$ 同胚的子图
瓦格纳(Wagner)定理：一个图是平面图当且仅当它的任何子图都不能通过边的收缩得到$K_5$ 或 $K_{3,3}$
从库拉托斯基(Kuratowski)定理到瓦格纳(Wagner)定理
假定图G不是平面图，则其包含与$K_5$ 或 $K_{3,3}$ 同胚的子图，将这些同胚子图中度为二的节点去除，则可以收缩得到$K_5$ 或 $K_{3,3}$，从而顺利切换到了瓦格纳定理
同胚 (Homeomorphic)
如果两个图可以从同一个原始图通过 “在边上插入度为2的新顶点” 得到，那么这两个图同胚
无限可数平面图的证明：如果G是可数图，且其的每个有限子图为平面图，则G是平面图
证明过程
把 $G$ 的顶点按序列列出为 $v_1,v_2,\dots$。令 $G_i$ 为$v_1,\dots,v_i$ 所诱导的有限子图，则每个 $G_i$ 都可平面嵌入。
对于每个 $i$，记 $E_i$ 为 $G_i$ 的所有平面嵌入（按顶点处的环序或同胚类计）。注意每个 $E_i$ 是有限的（因为每个顶点的循环顺序是有限的），且若 $e \in E_i$ 与 $e’ \in E_{i+1}$ 满足 $e’$ 限制到前 $i$ 个顶点时等于 $e$，则称 $e’$ 是 $e$ 的延拓。
构造分层有向图（或有根的有限分支树）$T$：顶点集为 $\bigcup_i E_i$，只在相邻层间连接“延拓”关系。从任一层出发出度有限且层数无限，所以 $T$ 是一棵无限且有限分支的树。由柯尼希引理（König’s lemma）可知，$T$ 上存在无限向下路径：
\(e_1 \to e_2 \to e_3 \to \cdots, \qquad e_i \in E_i,\)
其中每个 $e_{i+1}$ 都延拓 $e_i$。
于是对任意 $i$，$e_i$ 给出了 $G_i$ 的无交嵌入，且这些嵌入相互兼容。将这些兼容嵌入按层取并（对每个顶点/边取某一层以后固定的图像），得到对整个 $G$ 的映射。任一有限子图落在某个 $G_i$ 中，因此其图像无交；故全图的映射也是无交的平面嵌入。因此 $G$ 为平面图。
欧拉等式
面(face)的定义：被图的顶点和边划分出的一个个独立区域，被称为面(face)，无限面(infinite face) 则是唯一不被包围的、包含图外所有无限延伸的区域。
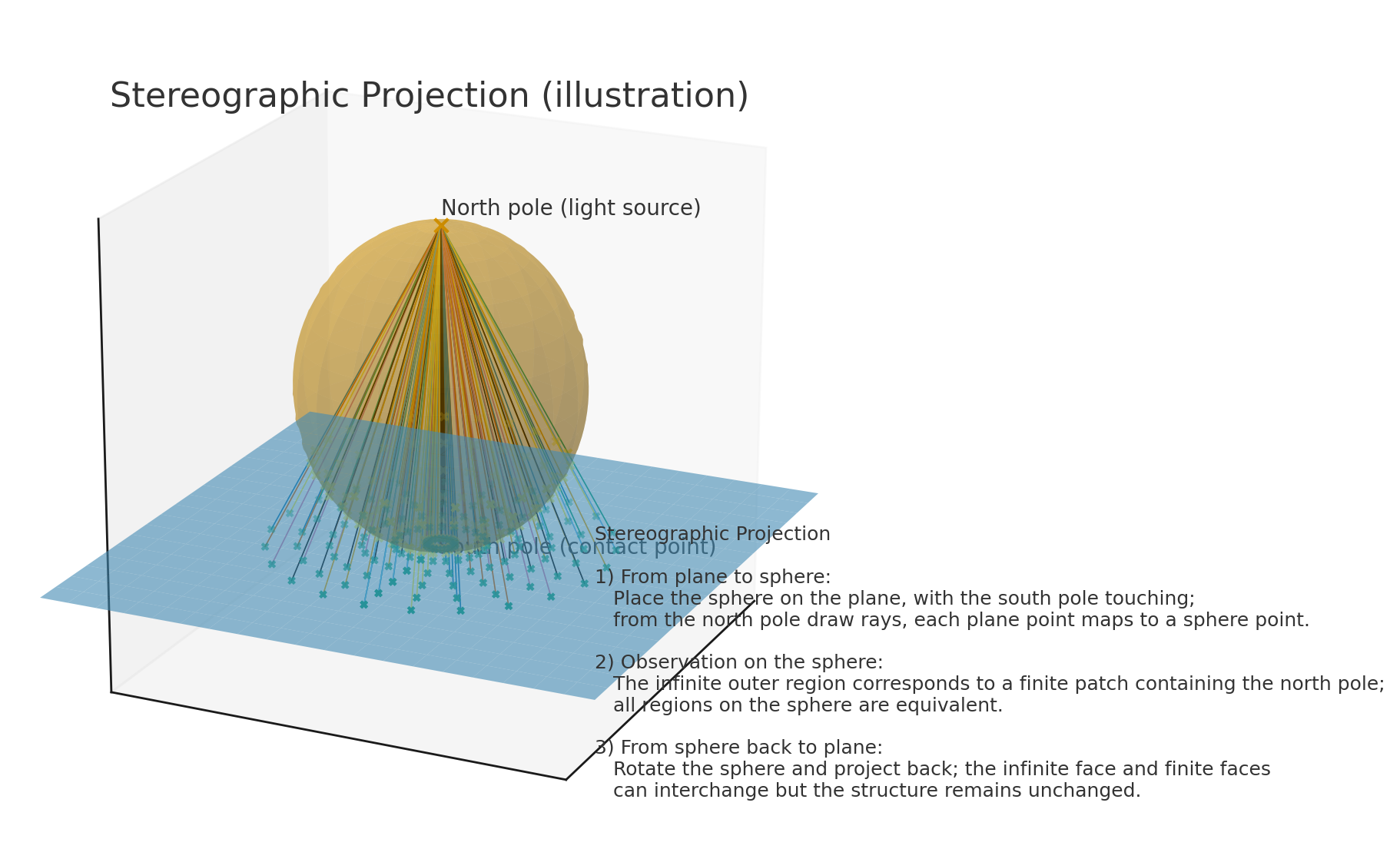
球极平面投影(stereographic projection)
无限面和其它面是平等的，这里用球极平面投影(stereographic projection)可以证明，步骤如下：
- 从平面到球面： 拿一个球体，把它放在我们画好的平面图上，让球的“南极”与平面接触；从球的“北极”点亮一盏灯。平面图上的每一个点和每一条线，都会在球的表面上投下影子；我们就把整个平面图“画”到了球面上
- 在球面上的观察： 当图被画到球面上之后，无限的外部区域，在球面上变成了包含“北极”点的一块有限的“补丁”；球面被图的线条分成了多个小块，所有这些面在地位上都是平等的，就像足球上的色块一样，没有哪个是“外面”的，此时也没有“无限面”了
- 从球面回到平面： 现在可以随意转动这个球再进行一次相反的投影；结果无边界的无限面和普通的内部面发生内部互换，但实际整体上并没有变化
欧拉公式(Euler’s Formula)： 令G为平面连通图的平面画法，$n,m,f$分别为该图的顶点、边和面，则三者满足：
\[n-m+f=2\]上述公式的证明并不难，采用归纳法即可完成证明。
平面连通图(Connected Plannar Graph)
平面连通图并不是说该图就是平面的，这是一个性质或潜力的描述。它指的是一个图有没有可能被画在一个平面（比如一张纸）上，并且所有的边除了在顶点处之外，互相不交叉。一个图是 “平面图(Plannar Graph)” ，不代表它现在画出来的样子就没有交叉。它仅仅意味着存在至少一种能让它没有交叉的画法。如果一个图不是平面图（比如 $K_5$），那么它就不可能有 “平面画法(Plane Drawing)” 。如果一个图是平面图，那么它至少有一个“平面画法”。
多面体图引理及其推广： 对于多面体图及相关推广有两条引理
- 令G为多面体图，其满足等式 $n-m+f=2$
- 令G为平面图，其具有n个节点、m条边、f个面和k个连通分量，则有等式 $n-m+f=k+1$ (证明方法：对不同的连通分量分别应用欧拉公式，然后进行整合)
简单图的一些引理和定理：
- 如果G是简单连通平面图，且有n(大于等于3)个节点和m条边，则 $m \le 3n-6$；如果G不存在三角形结构，则 $m \le 2n-4$
- $K_5$和$K_{3,3}$都是非平面图
- 任意简单平面图G中，至少存在一个节点的度小于等于5
概念回顾：简单图、连通图、平面图
简单图是无重边、无自环的图，连通图是任意两点可达的图，平面图是边不交叉的图
图的厚度(thickness)： 将图G所有边分解成最少的若干个平面子图所需的数量
对于一个简单图，假设其有n(大于等于3)个节点和m条边，则有如下不等关系：
\[t(G) \ge \lceil \frac{m}{3n-6} \rceil , \quad t(G) \ge \lfloor \frac{m+3n-7}{3n-6} \rfloor\]关键不等式
对于向上取整和向下取整之间，满足不等式：
\(\lceil \frac{a}{b} \rceil = \lfloor \frac{a+b-1}{b} \rfloor\)
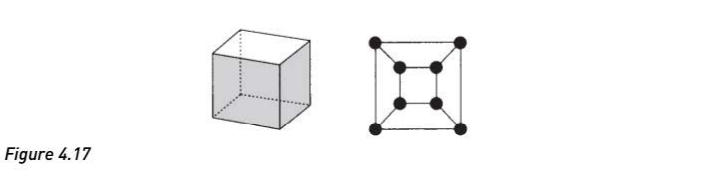
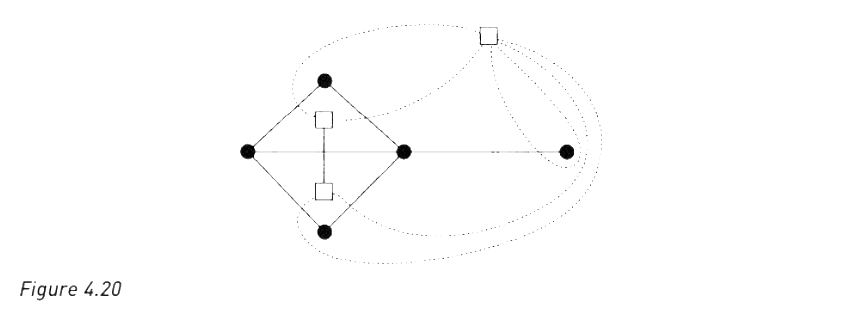
对偶图(Dual Graph)
构架过程：给定一个平面图 $G$ ，可以构建图 $G$ 的对偶图，记作 $G^*$ ，其构建方式分为两步：
- 在图 $G$ 内的每个面内选择点 $v^$ ，作为 $G^$ 的顶点
- 针对图 $G$ 的每条边，绘制边 $e^$ 穿过图 $G$ 的一条边 $e$ 、连接位于 $e$ 所毗邻的面 $f$ 中的顶点 $v^$
对偶图的一些关系
如果 $G$ 为平面图且连通，则 $G^$ 也为平面图且连通，同时图 $G$ 和图 $G^$ 在顶点、边和面上存在一些关系。
令图 $G$ 为具有 $n$ 个顶点、 $m$ 条边、 $f$ 个面的连通平面图，令其的对偶图具有 $G^$ 具有 $n^$ 个顶点、 $m^$ 条边、 $f^$ 个面，则有下述三个等量关系，其中第三个可以通过欧拉公式证明：
\[n^*=f, m^*=m, f^*=n\]同构性质：当 $G$ 为平面图且连通，则 $G^{**}$ 和 $G$ 是同构的