机器学习与算法交易(四): 更复杂的机器学习与量化模型

⽤于波动率预测和统计套利的时间序列模型

本部分，我们将构建动态线性模型，以明确表示时间，并纳⼊在特定时间间隔或滞后期观测到的变量。时间序列数据的⼀个关键特征是其序列顺序：我们的数据不是像横截⾯数据那样的单个观测值的随机样本，⽽是⼀个我们⽆法重复的随机过程的单次实现。我们的⽬标是识别时间序列中的系统性模式，以帮助我们预测该时间序列未来的⾏为。

用于诊断和特征提取的工具

时间序列有一系列离散数值组成，可以被建模为一组随机过程：

\[t_i \to y(t_i) \ for \ \{ t_i \| i=1,\cdots,T \}\]

在不同时间点$t_{i’}t_{j’}$之间的周期数$\Delta t=t_i-t_j$称为滞后，每个时间序列有T-1个不同的滞后。在该背景下，滞后值序列${ y_{t-1},\cdots,y_{t_{T}} }$一起作为输入。

如果一个时间序列是一系列独立同分布(IID)的随机变量$\epsilon_{t}$，且具有有限的均值和方差，则它被称为白噪声。特别的，如果这些随机变量服从均值为0，恒定方差为$\sigma$的正态分布，该序列被称为白噪声。

如果一个时间序列写成过去的扰动项$\epsilon_t$和序列均值$\mu$的加权和，则其为线性的：

\[y_t=\mu+\sum\limits_{i=0}^{\infty}a_{i}\epsilon_{t-i},a_0=1,\epsilon \sim i.i.d\]

时间序列分析的⼀个关键⽬标是理解由系数$a_i$驱动的动态⾏为。时间序列分析提供了针对此类数据的⽅法，旨在提取有⽤的模式，进⽽帮助我们构建预测模型。

时间序列模式的分解

时间序列数据通常包含多种模式的混合，这些模式可以分解为⼏个组成部分。具体来说，⼀个时间序列常常将趋势、季节性和周期等系统性成分与⾮系统性的噪声结合在⼀起。这些成分可以建模为线性组合（例如，当波动不依赖于序列的⽔平时），也可以建模为⾮线性的乘法形式。

滚动窗⼝统计与移动平均

鉴于时间序列数据的顺序性，为给定⻓度的周期计算常⻅的描述性统计数据是很⾃然的做法。其⽬标是检测序列是稳定还是随时间变化，并获得⼀个平滑的表示，在滤除噪声的同时捕捉系统性特征。

滚动窗⼝统计服务于这⼀过程：它们⽣成⼀个新的时间序列，其中每个数据点都代表了为原始数据某个周期计算的汇总统计量。移动平均是最常⻅的例⼦。原始数据点可以以相等的权重参与计算，也可以（例如）赋予近期数据点更⾼的权重。指数移动平均会递归地计算权重，这些权重会随着数据点在时间上的推移⽽衰减。新的数据点通常是所有先前数据点的汇总，但也可以根据⼀个围绕的窗⼝来计算。

早期的预测模型包括带有指数权重的移动平均模型，称为指数平滑模型。我们将在后⾯再次遇到移动平均，它是线性时间序列的关键构建模块。依赖指数平滑⽅法的预测使⽤的是过去观测值的加权平均，其中权重会随着观测值变旧⽽呈指数级衰减。因此，越近的观测值获得的权重越⾼。这些⽅法在没有⾮常复杂或突变模式的时间序列中很受欢迎。

自相关性的衡量

自相关性系数$\rho_{k}$衡量的是由给定滞后期$k$分隔的时间序列值之间的线性关系程度：

\[\rho_{k}=\frac{\sum\limits_{t=k+1}^{T}(y_t-\bar{y})(y_{t-k}-\bar{y})}{\sum\limits_{t=1}^{T}(y_t -\bar{y})^{2}}\]

因此，对于一个长度为$T$的时间序列，我们可以为其$T-1$个滞后期中的每一个计算一个自相关系数。自相关函数(ACF)滞后期大于1(即相隔超过一个时间步的观测值之间)的自相关，即反映了这些观测值之间的直接相关性，也反映了中间数据点的间接影响；偏⾃相关则移除了这种影响。还有⼀些算法可以根据偏⾃相关函数（PACF）和⾃相关函数（ACF）之间确切的理论关系，从样本⾃相关中估算出偏⾃相关。

如何诊断并实现平稳性

平稳时间序列的统计特性，如均值、⽅差或⾃相关，都与时间段⽆关，没有趋势或季节性效应；此外，描述性统计量在针对不同滚动窗⼝计算时，是恒定的或不随时间发⽣显著变化。平稳时间序列会回归其均值，其偏差具有恒定的振幅，⽽短期波动在统计意义上总是相似的。

更正式地说，严平稳性要求时间序列观测值任何⼦集的联合分布在所有矩上都与时间⽆关。因此，除了均值和⽅差，更⾼阶的矩（如偏度和峰度）也需要保持恒定，⽆论不同观测值之间的滞后如何。

转换时间序列以实现平稳性

为了满⾜许多时间序列模型的平稳性假设，我们需要对原始序列进⾏转换，这通常需要⼏个步骤。常⻅的转换⽅法包括使⽤(⾃然)对数将指数增⻓模式转换为线性趋势并稳定⽅差。

缩减（Deflation）是指将⼀个时间序列除以另⼀个导致趋势⾏为的序列，例如，将名义序列除以价格指数，以将其转换为实际度量。如果⼀个序列能够回归到稳定的⻓期线性趋势，那么它就是趋势平稳的。通常可以通过线性回归拟合趋势线并使⽤残差来使其平稳。这意味着将时间索引作为⾃变量纳⼊线性回归模型，并可能结合对数转换或平减处理。

在许多情况下，仅去除趋势并不⾜以使序列平稳。相反，我们需要将原始数据转换为⼀个周期与周期之间和/或季节与季节之间差异的序列。换句话说，我们使⽤相邻数据点或季节性滞后值相互减法的结果。请注意，当这种差分应⽤于经过对数转换的序列时，其结果在⾦融背景下代表瞬时增⻓率或回报率。

单位根和随机游走
在时间序列建模中，存在单位根会导致序列非平稳（如随机游走），常需通过差分（包括一阶差分和季节性差分）来实现平稳化。单位根可用ADF 检验等统计方法诊断，检验结果指导差分次数和滞后阶数的选择。除了整数阶差分，还可用分数阶差分保留更多长期信息。并提供了基于自相关特征判断是否需差分及是否过度差分的经验法则。

单变量时间序列模型

单变量时间序列模型将时间序列的当前值与该序列的滞后值、当前噪声以及可能存在的过去噪声项的线性组合关联起来。

构建自回归模型

一个$p$阶的AR模型旨在捕捉时间序列在不同滞后期的值之间的线性依赖关系，可写成如下形式：

\[AR(p):y_t=\phi_0+\epsilon_t+\sum\limits_{i=1}^{p}\phi_i y_{t-i}\]

该模型具有特征方程：

\[1-\sum\limits_{i=1}^{p}x^{i}=0\]

该方程解的倒数就是特征根，如果所有根的绝对值小于1，则$AR(p)$平稳，否则不平稳。对于平稳序列，多步预测将收敛于序列的均值。

确定模型阶数

在实践中，挑战在于确定滞后项的合适阶数p，ACF估算的是不同滞后阶数观测值之间的自相关性，⽽这种⾃相关性是由直接和间接的线性依赖关系共同导致的。如果⼀个k阶的AR模型是正确的模型，那么ACF将显示出直到滞后k阶的显著序列相关性，并且由于线性关系的间接影响所产⽣的惯性，这种相关性会延伸到后续的滞后阶数，直到影响减弱并最终逐渐消失。⽽PACF只衡量给定滞后间隔的观测值之间的直接线性关系，因此它不会反映出超过k阶的滞后相关性。

诊断模型拟合

如果模型恰当地捕捉了不同滞后阶之间的线性依赖关系，那么残差应类似于⽩噪声，并且⾃相关函数（ACF）图应凸显出不存在显著的⾃相关系数。

Ljung-Box Q 统计量也让我们能够检验残差序列是否服从⽩噪声的假设。其原假设是所有$m$序列的相关系数为0，备择假设为一些系数非0，该检验统计量根据不同滞后阶$k$的样本自相关系数$\rho_{k}$计算得出，并服从分布：

\[Q(m)=T(T+2)\sum\limits_{t=1}^{m}\frac{\rho_{l}^{2}}{T-l}\]

构建移动平均模型

$MA(q)$模型在⼀个类似回归的模型中使⽤$q$个过去的扰动项，⽽不是时间序列的滞后值，其形式如下：

\[MA(q):y_t=c+\epsilon_t+\sum\limits_{i=1}^{p}\theta_i \epsilon_{t-i},\epsilon \sim i.i.d\]

确定滞后阶数

由$ MA(q) $过程⽣成的时间序列是由先前$q$个模型预测的残差驱动的。因此，$MA(q) $过程的⾃相关函数(ACF)将在滞后阶数达到$log \ q$之前显示出显著的系数，然后急剧下降，因为模型就是这样假设序列值⽣成的。

AR 模型与 MA 模型之间的关系

一个$AR(p)$模型总能通过重复代换表示为$MA(\infty)$过程；当$MA(q)$过程的系数满足某些大小约束时，它也变得可逆，并可以表示为$AR(\infty)$过程。⾃回归移动平均（ARIMA）模型结合了 AR(p) 和 MA(q) 过程，以利⽤这些构建模块的互补性，并简化模型开发。它们通过使⽤更紧凑的形式和减少参数数量来实现这⼀点，从⽽降低过拟合的⻛险。

对差分序列建模

不进⾏差分的模型假设原始序列是平稳的，包括均值回归。它通常包含⼀个常数项，以允许⾮零均值。进⾏⼀阶差分的模型假设原始序列具有恒定的趋势，因此应包含⼀个常数项。⼀个进⾏⼆阶差分的模型假设原始序列具有时变趋势，因此不应包含常数项。

当然还可以通过ARMAX添加特征或通过SARIMAX加入季节性差分，进一步提升模型效果。进一步的，对模型进行更新，可以得到效果更好的ARCH和GARCH模型预测波动率。

多变量时间序列模型

多变量时间序列模型旨在同时捕捉多个时间序列的动态，并利⽤这些序列间的依赖关系来进⾏更可靠的预测。该模型允许其他时间序列的滞后值影响⽬标变量。这种影响适⽤于所有序列，从⽽产⽣复杂的相互作⽤。除了可能提供更好的预测外，多变量时间序列还⽤于深⼊了解序列间的相互依赖关系。

向量自回归模型

向量自回归模型在$k$个时间序列和$p$阶下表示为：

\[{\bf{y}}_{t}={\bf{c}}+\boldsymbol{\epsilon}_t+\sum\limits_{i=1}^{p}{\bf{A}}_i {\bf{y}}_{t-i}\]

VAR§模型也要求平稳性，因此单变量时间序列建模的初始步骤同样适⽤。如果$k$个序列中的部分或全部是单位根⾮平稳的，它们可能存在协整关系。这个将单位根概念扩展到多个时间序列的含义是，两个或多个序列的线性组合是平稳的，因此具有均值回归特性。

协整
协整就是在多个各自非平稳(I(1))的时间序列中，找出能组合成平稳(I(0))序列的线性关系，目的是避免伪回归并捕捉均值回归机会，可用 Engle–Granger（两步法，适合成对）或 Johansen（适合多变量）检验来计算，常用于统计套利、配对交易等量化策略中，以价差偏离均值时建仓、回归均值时平仓。

贝叶斯机器学习

⻉叶斯统计学使我们能够量化未来事件的不确定性，并在新信息到来时以⼀种有原则的⽅式修正我们的估计。这种动态⽅法能很好地适应⾦融市场不断变化的特性。当相关数据较少，⽽我们需要系统性地整合先验知识或假设的⽅法时，它尤其有⽤。

贝叶斯机器学习的工作原理

如何根据经验证据更新假设

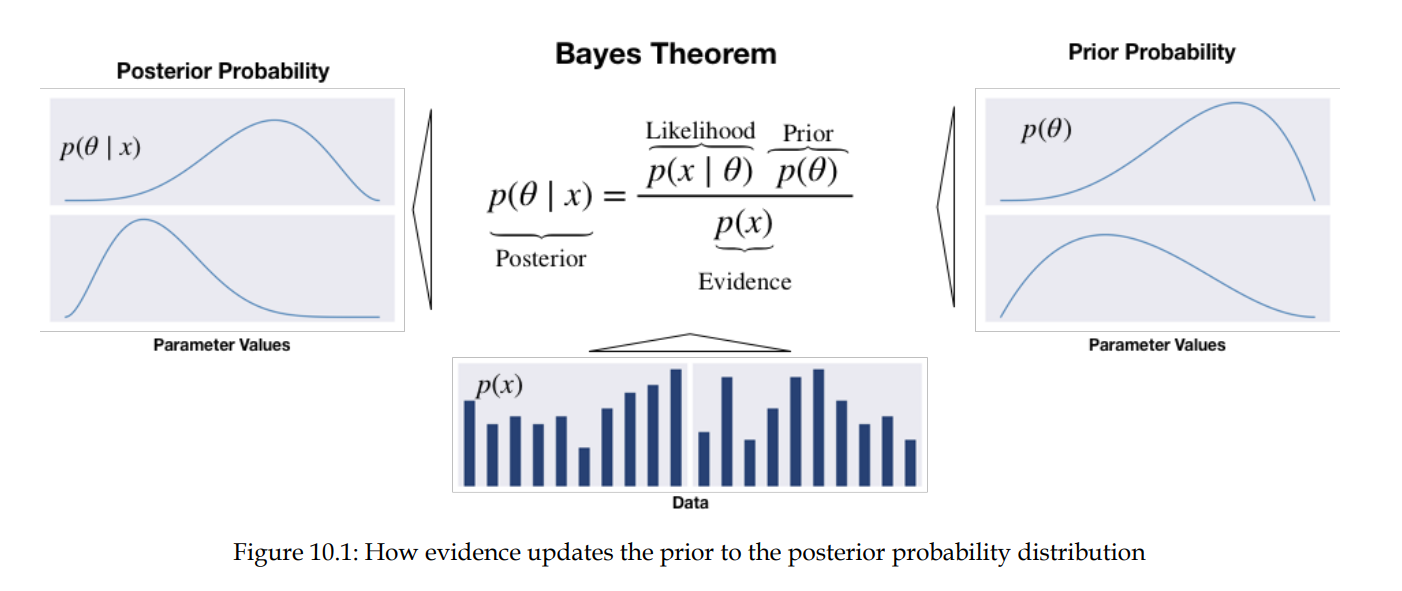
⻉叶斯假设是以概率分布的形式表达，⽽⾮参数值。因此，频率派推断侧重于点估计，⽽⻉叶斯推断则得出概率分布。后验概率是先验概率与似然的乘积，再除以证据。因此，它反映了假设的概率分布，该分布在考虑了先验假设和数据后进⾏了更新。从另⼀个⻆度看，后验概率是应⽤链式法则的结果，⽽链式法则⼜将数据和参数的联合分布进⾏因式分解。

精确推断：最⼤后验估计

⻉叶斯法则在精确计算后验概率⽅⾯的实际应⽤相当有限。这是因为分⺟中证据项的计算极具挑战性。证据项反映了在所有可能的参数值下观测到数据的概率。它也被称为边际似然，因为它需要通过对参数分布进⾏求和或积分来“边缘化”参数的分布。这通常只在参数数量少、取值范围⼩的离散参数等简单情况下才可能实现。最⼤后验概率（MAP）估计利⽤了这样⼀个事实：证据项是⼀个常数因⼦，它对后验概率进⾏缩放以满⾜概率分布的要求。

如何选择先验

先验概率应反映关于参数分布的知识，因为它会影响最⼤后验概率（MAP）的估计。如果不能确定先验概率，我们就需要做出选择，⽽通常会有⼏个合理的选项。总的来说，⼀个好的做法是证明先验选择的合理性，并通过测试其他备选⽅案是否会得出相同结论来检验其稳健性。

在机器学习模型的背景下，先验可以被看作是⼀种正则化项，因为它限制了后验可以取的值。例如，先验概率为零的参数不会成为后验分布的⼀部分。通常，更多好的数据能得出更强的结论，并减少先验的影响。

先验分布有以下⼏种类型：

• 客观先验旨在最⼤化数据对后验分布的影响。如果参数分布未知，我们可以在相关参数值范围内选择⼀个⽆信息先验，例如均匀分布，也称为平坦先验。
• 相⽐之下，主观先验旨在将模型外部的信息纳⼊估计中。
• 经验先验结合了⻉叶斯⽅法和频率派⽅法，并利⽤历史数据来消除主观性，例如，通过估计各种矩来拟合⼀个标准分布。使⽤每⽇回报的某个历史平均值，⽽不是对未来回报的某种信念，就是⼀个简单经验先验的例⼦。

共轭先验：保持推断的简洁性

如果后验分布与先验分布属于同⼀类或同⼀族分布（只是参数不同），那么该先验分布相对于似然函数就是共轭的。例如，当先验和似然都服从正态分布时，后验也服从正态分布。先验和似然的共轭性意味着后验存在⼀个闭式解，这简化了更新过程，并避免了使⽤数值⽅法来近似后验的需要。此外，得到的后验可以作为下⼀次更新步骤的先验。

当数据由具有特定成功概率的伯努利⼆元随机变量组成时，重复试验中的成功次数遵循⼆项分布。其共轭先验是⻉塔分布，⽀撑区间为$[0,1]$，并有两个形状参数来为成功概率建模任意的先验分布。因此，后验分布也是⼀个⻉塔分布，我们可以通过直接更新参数来推导。

在实践中，共轭先验的使⽤仅限于低维情况。此外，简化的最⼤后验（MAP）⽅法虽然避免了计算证据项，但有⼀个关键缺点，即使在证据项可⽤的情况下也是如此：它不返回⼀个分布，因此我们⽆法从中推导出不确定性的度量，也⽆法将其⽤作先验。因此，我们需要借助数值⽅法和随机模拟进⾏近似推断，⽽⾮精确推断。

确定性与随机性近似推断

对于⼤多数具有实际意义的模型，我们都⽆法通过解析⽅法推导出精确的后验分布，也⽆法计算出潜变量的期望值。

• 对于连续变量，积分可能没有封闭解，⽽空间的维度和被积函数的复杂性可能导致⽆法进⾏数值积分。
• 对于离散变量，边缘化需要对隐藏变量的所有可能配置进⾏求和。虽然这在理论上总是可⾏的，但在实践中我们常常发现，隐藏状态的数量可能呈指数级增⻓，导致计算成本过高。

基于⻢尔可夫链蒙特卡洛（MCMC）抽样的随机技术，已使⻉叶斯⽅法在许多领域得到普及。它们通常具有收敛到精确结果的特性。在实践中，抽样⽅法的计算量可能很⼤，通常仅限于⼩规模问题。被称为变分推断或变分⻉叶斯的确定性⽅法，基于对后验分布的解析近似，并且能够很好地扩展到⼤型应⽤中。

⻢尔可夫链蒙特卡洛抽样(MCMC)

抽样需要尽可能确保独立，但是⼀个实际的挑战在于，由于分布是未知的，如何确保独⽴抽样。⾮独⽴样本可能仍然是⽆偏的，但往往会增加估计量的⽅差，因此与独⽴样本相⽐，需要更多的样本才能获得同样精确的估计。随着维度的增加，状态的数量会呈指数级增⻓，因此从多元分布中抽样对计算的要求⾮常⾼。基于MCMC的一些⽅法变体则可以简化这一过程。

⻢尔可夫链是⼀种动态随机模型，它描述了⼀系列由转移概率连接的状态上的随机游⾛。⻢尔可夫性质规定了该过程没有记忆性，下⼀步只取决于当前状态。换句话说，这取决于现在、过去和未来是否相互独⽴，也就是说，除了我们从当前状态中了解到的信息外，关于过去状态的信息⽆助于预测未来。

蒙特卡洛⽅法依赖于重复随机抽样来近似那些可能是确定性的但⽆法求得精确解析解的结果。它是在曼哈顿计划期间为估算原⼦层⾯的能量⽽开发的，并为了保密⽽获得了这个经久不衰的代号。

MCMC及其各类变体的过程通常如下：

• 从当前位置开始
• 从一个提议分布中抽取一个新位置
• 根据数据和先验分布评估新位置的概率
  • 如果可能性足够大，则移动到新位置
  • 否则保持在当前位置
• 重复直至迭代次数用完
• 返回所有接受的位置

吉布斯抽样

吉布斯抽样将多变量抽样简化为⼀系列⼀维抽样。它从某个起点开始，迭代地保持$n-1$个变量不变，同时对第$n^{th}$个变量进⾏抽样。然后，它将这个样本纳⼊考虑并重复此过程。该算法⾮常简单且易于实现，但会产⽣⾼度相关的样本，从⽽减慢收敛速度。其顺序性也使其⽆法并⾏化。

Metropolis-Hastings 抽样

Metropolis-Hastings 算法根据其当前状态随机提出新位置。这样做是为了有效地探索样本空间，并减少样本相对于吉布斯采样的相关性。为确保从后验分布中采样，该算法使⽤先验和似然的乘积来评估提议，该乘积与后验成正⽐。它以⼀定的概率接受提议，该概率取决于提议的结果与当前样本对应值的相对关系。

提议评估⽅法的⼀个关键优势是，它使⽤的是后验的⽐例评估⽽⾮精确评估。然⽽，它可能需要很⻓时间才能收敛。这是因为与后验⽆关的随机移动会降低接受率，导致⼤量的步骤只产⽣少量（可能相关的）样本。可以通过减⼩提议分布的⽅差来调整接受率，但由此产⽣的更⼩步⻓意味着探索范围更⼩。

哈密顿蒙特卡洛(NUTS)算法

哈密顿蒙特卡洛（HMC）是⼀种混合⽅法，它利⽤了似然梯度的⼀阶导数信息。借此，它提出新的状态进⾏探索，并克服了 MCMC 的⼀些挑战。此外，它还引⼊了动量来有效地在后验分布中“跳跃”。因此，它⽐简单的随机游⾛ Metropolis 算法或吉布斯采样能更快地收敛到⾼维⽬标分布。⽆ U 形转弯采样器（NUTS，Hoffman and Gelman 2011）则是⼀种⾃调整的 HMC 扩展算法。

变分推断(VI)与⾃动微分

变分推断（VI）是⼀种通过优化来近似概率密度的机器学习⽅法。在⻉叶斯理论中，它通过以下⽅式来近似后验分布：

• 选择⼀个参数化的概率分布族
• 以库尔⻉克-莱布勒散度(Kullback-Leibler divergence)来衡量，找到该族中与⽬标最接近的成员

与 MCMC 相⽐，变分⻉叶斯收敛速度更快，对⼤数据的扩展性也更好。MCMC ⽤⻢尔可夫链中的样本来近似后验分布，这些样本最终会任意逼近⽬标；⽽变分算法则⽤优化的结果来近似后验分布，但不能保证与⽬标完全⼀致。变分推断的缺点是需要针对特定模型进⾏推导，并实现量身定制的优化程序，这减缓了其⼴泛应⽤。

变分推断更适⽤于⼤型数据集，例如数亿份⽂本⽂档，这样我们就可以快速探索多种模型。相⽐之下，MCMC 在较⼩的数据集上，或者在时间和计算资源限制较少的情况下，会得出更准确的结果。例如，如果你花了 20 年时间收集了⼀个⼩⽽昂贵的数据集，确信你的模型是合适的，并且需要精确的推断，那么 MCMC 将是⼀个不错的选择。

随机森林

决策树：从数据中学习规则

决策树是⼀种机器学习算法，它根据从数据中学习到的决策规则来预测⽬标变量的值。通过改变指导树学习规则的⽬标函数，该算法既可以应⽤于回归问题，也可以应⽤于分类问题。

决策树如何学习

决策树学习并按顺序应⽤⼀系列规则，将数据点分割成⼦集，然后对每个⼦集做出⼀个预测。这些预测基于应⽤给定规则序列后产⽣的训练样本⼦集的输出值。分类树直接预测从相对类别频率估算出的概率或多数类的值，⽽回归树则根据可⽤数据点的输出值的平均值来计算预测结果。

每⼀条规则都依赖于⼀个特定的特征，并使⽤⼀个阈值将样本分成两组，⼀组的该特征值低于阈值，另⼀组则⾼于阈值。⼆叉树⾃然地表示了模型的逻辑：根节点是所有样本的起点，节点代表决策规则的应⽤，数据沿着边移动，被分割成更⼩的⼦集，直到到达叶节点，模型在此处做出预测。

构建回归树

给定训练集，算法遍历$p$个预测变量${ X_{1’},\cdots,X_{p’} }$和$n$个可能的切分点$s_1,\cdots,s_n$，以找到一个最优组合。最优规则将特征空间划分为两个区域${ X | X_i \le s_j }$和${ X | X_i > s_j }$，从⽽使基于训练⼦集的预测能够最⼤程度地减少相对于当前节点的残差平⽅和。

构建分类树

分类树的⼯作原理与回归树类似，但由于结果是分类性质的，因此需要采⽤不同的⽅法来进⾏预测和衡量损失。回归树使⽤相关训练样本结果的均值来预测分配到叶节点的观测值的响应，⽽分类树则使⽤众数，即相关区域中训练样本最常⻅的类别。分类树还可以根据相对类别频率⽣成概率性预测。

过拟合与正则化

决策树有很强的过拟合倾向，尤其是当数据集的特征数量相对于样本数量较多时。如前⼏章所述，过拟合会增加预测误差，因为模型不仅学习了训练数据中包含的信号，还学习了其中的噪声。

有多种⽅法可以应对过拟合的⻛险：

• 降维：通过⽤更少、信息量更⼤、噪声更低的特征来表示现有特征，从⽽改善特征与样本的⽐率
• 集成模型：结合多棵树，同时在建树过程中引⼊随机性
• 树剪枝：通过删除那些价值不⼤但会增加模型⽅差的节点或树的整个部分来实现这⼀⽬的

从特征重要性中获得洞⻅

决策树不仅可以通过可视化来检查给定特征的决策路径，还可以总结每个特征对模型为拟合训练数据⽽学习到的规则所做的贡献。

特征重要性衡量了每个特征产⽣的分割在多⼤程度上有助于优化模型⽤于评估分割质量的指标，在本例中即基尼不纯度。⼀个特征的重要性被计算为该指标的（归⼀化）总减少量，并考虑了受分割影响的样本数量。因此，在决策树中较早使⽤的特征，其节点往往包含更多样本，通常被认为具有更⾼的重要性。

随机森林：让决策树更可靠

决策树的⽤处不仅在于其透明度和可解释性，它们还是更强⼤的集成模型的基础构件。集成模型会组合许多单独的决策树，并通过随机改变其设计来解决我们刚刚讨论的过拟合问题。

集成模型性能更优的原因

集成学习是指将多个机器学习模型组合成⼀个新模型，旨在做出⽐任何单个模型都更好的预测。更具体地说，集成模型会整合多个基础评估器的预测结果，这些评估器使⽤⼀种或多种学习算法进⾏训练，⽬的是减少这些模型单独产⽣的泛化误差。

要让集成学习实现这⼀⽬标，其包含的单个模型必须：

• 准确：表现优于朴素基线(如样本均值或类别⽐例)
• 独⽴：以不同的⽅式⽣成预测，从⽽产⽣不同的误差

集成⽅法是机器学习算法中最成功的⼀类，尤其是在处理标准数值数据⽅⾯。⼤型集成模型在机器学习竞赛中⾮常成功，它们可能由许多不同的单个模型组成，这些模型通过⼿动或使⽤另⼀种机器学习算法进⾏组合。组合不同模型做出的预测有⼏个缺点，包括可解释性降低，以及训练、预测和模型维护的复杂度和成本更⾼。因此，在实践中，⼤规模集成所带来的微⼩精度提升可能不值得额外的成本。

⾃助聚合

对更⼤规模的观测值集进⾏平均可以降低⽅差。因此，降低模型⽅差及其泛化误差的⼀个⾃然⽅法是，从总体中收集许多训练集，在每个数据集上训练⼀个不同的模型，然后对得出的预测结果进⾏平均。

Bagging 指的是对 bootstrap 样本进⾏聚合，⽽ bootstrap 样本是含放回的随机样本。这种随机样本的观测值数量与原始数据集相同，但由于是放回抽样，可能包含重复的观测值Bagging 提升了预测准确性，但降低了模型的可解释性，因为它⽆法再通过可视化决策树来理解每个特征的重要性。作为⼀种集成算法，Bagging ⽅法在这些⾃助采样样本上训练给定数量的基估计器，然后将其预测结果聚合为最终的集成预测。

随机森林的特征重要性

⼀个随机森林集成模型可能包含数百棵独⽴的决策树，但我们仍然可以从这些袋装模型中获得⼀个关于特征重要性的总体摘要度量。

对于给定的特征，其重要性得分是指因该特征上的分裂⽽导致的⽬标函数值的总减少量，并在所有树上取平均值。由于⽬标函数会考虑有多少特征受到分裂的影响，因此在树的顶部附近使⽤的特征会获得更⾼的分数，因为可⽤节点数量较少，但其中包含的观测值数量更多。通过对以随机⽅式⽣⻓的许多树进⾏平均，特征重要性估计的⽅差会减⼩，从⽽变得更加准确。